Special Product and Factoring
6.1 Basic Algebra/Factoring/Squares of BinomialsBinomial - An algebraic expression with exactly two terms.Square - Multiply a number by itself.FOIL - The product of two binomials is the sum of the products of the First terms, the Outer terms, the Inner terms, and the Last terms.Quantity -Total amount or number.(a+b)2 = a2 + 2ab + b2(a-b)2 = a2 - 2ab + b2NOTE: These equations will work if you substitute the first term for a and the second term for b. I find these equations easier to understand after the concept is learned using the three steps described below.Lesson 4 has shown you how to multiply binomials. In Lesson 5 we are going to learn how to square binomials. Squaring a binomial can be done using two different methods. The first method uses FOIL (refer to lesson 4). The second method is a shorter alternative to FOIL. The way we use the shortcut is to follow three simple steps.Step 1 Square the first term of the binomial.Step 2 Multiply the first term and last term of the binomial together and then double that quantity (in other words multiply by 2).Step 3 Square the last term of the binomial.Here is an example to follow.Using the binomial (x+6) we will square it creating the problem (x+6)2Step 1 Square the first term of the binomial.(x)2=x2Step 2 Multiply the first term and last term of the binomial together and then double that quantity (in other words multiply by 2).[(x)*(6)]*2 = (6x)*(2) = 12xStep 3 Square the last term of the binomial.(6)2 = 36Finally we put the three term we have acquired together and get the answer(x+6)2 = x2 + 12x + 36Let’s try one more problem that may be a more difficult.Let’s square the binomial (x2-4x) giving us (x2-4x)2Step 1 Square the first term of the binomial.(x2)2 = x4Step 2 Multiply the first term and last term of the binomial together and then double that quantity (in other words multiply by 2).*Notice we keep the negative sign with the second term[(x2)(-4x)]*2 = (-4x3)*(2) = -8x3Step 3 Square the last term of the binomial.(-4x)2 = (-4)2(x)2 = 16x2Our final answer will be the answers from the three steps combined(x2-4x)2 = x4 -8x3 + 16x2
6.2 Cube Of Binomial
A cubed binomial (sum) is equal to the cube of the first, plus three times the square of the first by the second, plus three times the first by the square of the second, plus the cube of the second.(a + b)3 = a3 + 3 · a2 · b + 3 · a · b2 + b3(x + 3)3 = x 3 + 3 · x2 · 3 + 3 · x· 32 + 33 == x 3 + 9x2 + 27x + 27A cubed binomial (difference) is equal to the cube of the first, minus three times the square of the first by the second, plus three times the first by the square of the second, minus the cube of the second.(a − b)3 = a3 − 3 · a2 · b + 3 · a · b2 − b3(2x − 3)3 = (2x)3 − 3 · (2x)2 ·3 + 3 · 2x· 32 − 33 == 8x 3 − 36 x2 + 54 x − 27Examples1(x + 2)3 = x3 + 3 · x2 · 2 + 3 · x · 22 + 23 == x3 + 6x2 + 12x + 82(3x − 2)3 = (3x)3 − 3 · (3x)2 · 2 + 3 · 3x · 22 − 23 == 27x 3 − 54x2 + 36x − 83(2x + 5)3 = (2x)3 + 3 · (2x)2 ·5 + 3 · 2x · 52 + 53 == 8x3 + 60 x2 + 150 x + 125
6.3 Sum And Difference Pattern
The other two special factoring formulas are two sides of the same coin: the sum and difference of cubes. These are the formulas:a3 + b3 = (a + b)(a2 – ab + b2) a3 – b3 = (a – b)(a2 + ab + b2)You'll learn in more advanced classes how they came up with these formulas. For now, just memorize them. First, notice that the terms in each factorization are the same; then notice that each formula has only one "minus" sign. For the difference of cubes, the "minus" sign goes with the linear factor, a – b; for the sum of cubes, the "minus" sign goes in the quadratic factor, a2 – ab + b2. Some people use the mnemonic "SOAP" for the signs; the letters stand for "same" as the sign in the middle of the original expression, "opposite" sign, and "always positive".a3 ± b3 = (a [same sign] b)(a2 [opposite sign] ab [always positive] b2)Whatever method helps you best keep these formulas straight, do it, because you should not assume that you'll be given these formulas on the test. You really should know them. Note: The quadratic part of each cube formula does not factor, so don't attempt it.When you have a pair of cubes, carefully apply the appropriate rule. By "carefully", I mean "using parentheses to keep track of everything, especially the negative signs". Here are some typical problems:Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved
- Factor x3 – 8
= (x – 2)(x2 + 2x + 4)
- Factor 27x3 + 1
- Factor x3y6 – 64
6.4 Trinomial Square
A trinomial that is the square of a binomial is called a TRINOMIAL SQUARE. Trinomials that are perfect squares factor into either the square of a sum or the square of a difference. Recalling that (x + y)2 = x2 + 2xy + y2 and (x - y)2 = x2 - 2xy + y2, the form of a trinomial square is apparent. The first term and the lastterm are perfect squares and their signs are positive. The middle term is twice the product of the square roots of these two numbers. The sign of the middle term is plus if a sum has been squared; it is minus if a difference has been squared.
The polynomial 16x2 - 8xy + x2 is a trinomial in which the first term, 16x , and the last term, y2, are perfect squares with positive signs. The square roots are 4x and y. Twice the product of these square roots is 2(4x)(y) = 8xy. The middle term is preceded by a minus sign indicating that a difference has beensquared. In factored form this trinomial is as follows:
16x2 - 8xy + y2 = (4x - y)2To factor the trinomial, we simply take the square roots of the end terms and join them with a plus sign if the middle term is preceded by a plus or with a minus if the middle term is preceded by a minus.
The terms of a trinomial may appear in any order. Thus, 8xy + y2 + 16x2 is a trinomial square and may be factored as follows:
8xy + y2 + 16x2 = 16x2 + 8xy + y2 = (4x + y)2Practice problems. Among the following expressions, factor those which are trinomial squares:

6.5 Common Factors in Polynomials
No matter how many terms a polynomial has, you always want to check for a greatest common factor (GCF) first. If the polynomial has a GCF, factoring the rest of the polynomial is much easier because once you factor out the GCF, the remaining terms will be less cumbersome. If the GCF includes a variable, your job becomes even easier.
When solving for x in a polynomial equation, if you forget to factor out the GCF, you may miss a solution, and that could mix you up in more ways than one! Without that solution, you could end up with an incorrect graph for your polynomial. And then all your work would be for nothing!
To factor the polynomial 6x4 – 12x3 + 4x2, for example, follow these steps:
- Break down every term into prime factors.This step expands the original expression to

- Look for factors that appear in every single term to determine the GCF.In this example, you can see one 2 and two x’s in every term:
 The GCF here is 2x2.
The GCF here is 2x2. - Factor the GCF out from every term in front of parentheses and group the remnants inside the parentheses.You now have
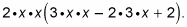
- Multiply each term to simplify.The simplified form of the expression you find in Step 3 is 2x2(3x2 – 6x + 2).To see if you factored correctly, distribute the GCF and see if you obtain your original polynomial. If you multiply the 2x2 inside the parentheses, you get 6x4 – 12x3 + 4x2. You can now say with confidence that 2x2 is the GCF.